Il y a pas mal de théories autour des pyramides d’Égypte et principalement celle de Kheops. Parmi ces théories, il y a l’utilisation de Pi, du nombre d’or et du mètre lors de la construction (≈2560 av. J.C.)
Quels unités de mesure utilisaient les Égyptiens de l’antiquité ?
Pour poser de bonnes bases à cette histoire, on va déjà regarder en détails les unités de mesures qu’utilisaient les égyptiens de l’antiquité. Je vous fais un résumé rapide des travaux de Jean-François Carlotti disponible ici. La plus grande unité de mesure est la coudée royale, toutes les autres en sont des fractions, c’est pourquoi j’indique la valeur approximative en centimètre ainsi que la valeur fractionnelle.
- Le doigt ≈ 1,87cm (1/28ème) : largeur d’un doigt.
- Le palme ≈ 7,5cm (1/7ème) : largeur de la paume de la main mesurée à la base des doigts.
- La main ≈ 9,375cm (1/7ème + 1/28ème) : largeur de la main plus le pouce.
- La sandale ≈ 10,5cm (5 doigts + 3/5) : on ne sait pas comment elle est mesurée.
- Le double palme ≈ 15cm (1/4 + 1/28ème) : deux largeurs de main.
- Le petit empan ≈ 22,5cm (1/4 + 1/27ème + 1/28ème) : distance entre le pouce et le petit doigt quand la main est ouverte au maximum.
- Le grand empan ≈ 26,25 cm (1/14ème) : on ne sait pas comment cette unité était mesurée.
- La coudée sacrée ≈ 30 cm (1/2 + 1/14ème) : distance entre le poignet et le creux du coude.
- La coudée remen ≈ 37,5 cm (1/2 + 1/7ème + 1/14ème) : distance entre l’épaule et le creux du coude.
- La petite coudée ≈ 45cm (3/4 + 1/14ème + 1/28ème) : distance entre l’extrémité du pouce et le creux du coude.
- Coudée Royale ≈ 52,3cm : distance entre le bout du majeur et le creux du coude.
Si vous voulez un peu plus de détails, voilà la représentation issue des travaux de Jean-François Carlotti.
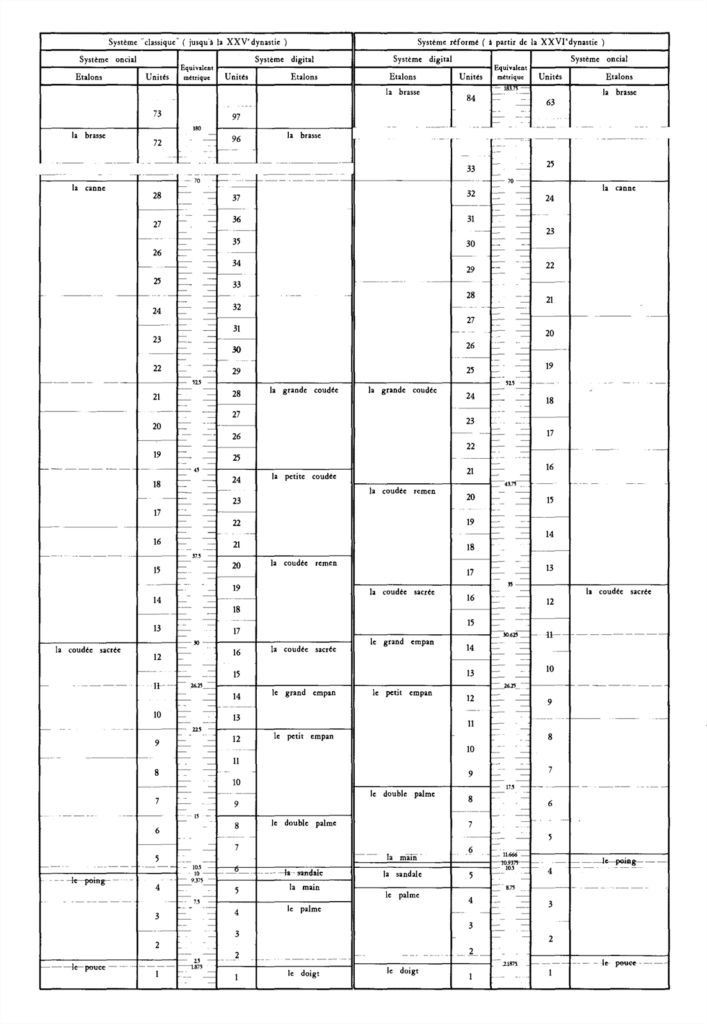
La coudée royale a varié durant l’histoire égyptienne et surtout ce n’est pas une unité de mesure exclusive à l’Égypte, c’est pour cette raison que l’on ne peut peut pas dire : « une coudée égale tant de centimètres ». Il faut préciser le type de coudée (royale, petite, sacrée, etc.) et surtout il faut la remettre dans son contexte géographique et historique. Comme cet article concerne la pyramide de Kheops, ça serait génial que l’on ait retrouvé une coudée en pierre ou en bois comme c’est régulièrement le cas, pour attester de la dimension exacte de cette fameuse coudée royale. Malheureusement nous n’avons pas retrouvé l’étalon de mesure utilisé pour ce bâtiment, mais il y a peut être un autre moyen d’en estimer sa dimension.
Comment calculer la coudée royale ?
Dans la pyramide de Kheops, il y a 3 chambres, la chambre souterraine, la chambre médiane (dite de la reine) et la chambre haute (dite du roi). La chambre haute est faite avec des dalles de granit et l’avantage de ce matériaux c’est qu’il bouge pas à travers le temps. Ce qui veut dire que les mesures que nous faisons aujourd’hui sont identiques à celles choisies à l’époque de la construction. L’architecte français Gilles Dormion a mesuré cette chambre, qui est un double carré, et a publié les plans dans son livre « La chambre de Chéops« .
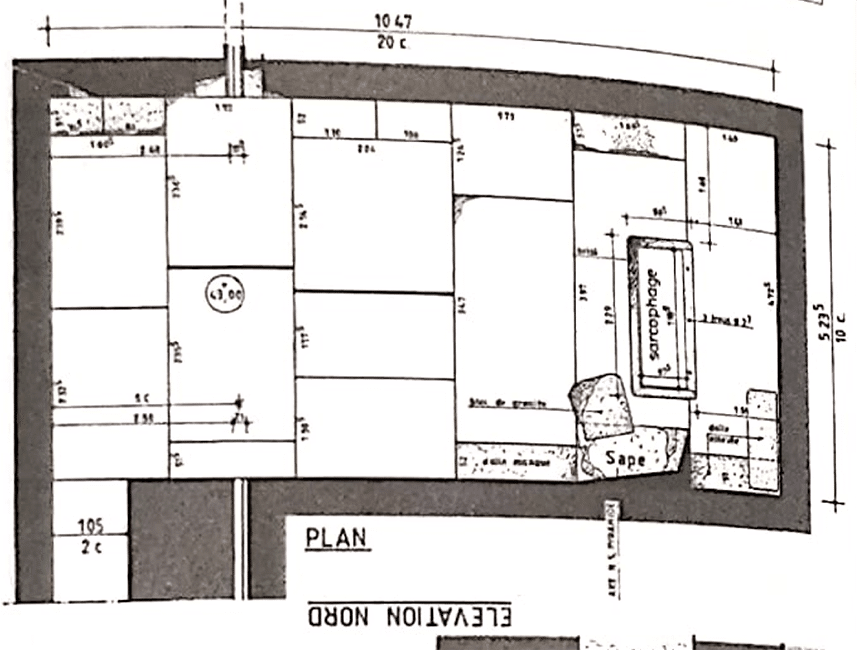
La chambre haute mesure 5,235 mètres de largeur et 10,47 mètres de longueur. En partant du principe que les égyptiens ont utilisé un nombre entier de coudée royale (CR), nous pouvons conclure que la chambre mesure 10 CR de largeur par 20 CR de longueur.
Pourquoi pas 11 × 22 ou 9 × 18 ?
D’après les coudées royales que les égyptologues ont retrouvé physiquement, nous savons que c’est une mesure qui varie de 52 cm à 54 cm pendant l’Égypte antique de la 1ère à la 26ème dynastie, cette dernière fera une grande réforme des unités de mesure.
Si la chambre faisait 9 CR de largeur ça nous donnerait une CR à 58 centimètres (5,235 ÷ 9 = 0,5816). Et si elle faisait 11 CR, cela nous donnerait une CR à 47 centimètres (5,235 ÷ 11 = 0,4759).
Donc, d’après les dimensions de la chambre haute, nous pouvons conclure que la coudée royale de la pyramide de Kheops mesure 0,5235 mètres.
C’est une donnée solide qu’il faut tout de même prendre avec précaution car ce raisonnement ne marche pas avec la hauteur de la chambre haute et surtout ne fonctionne pas du tout avec la chambre médiane (dite de la reine).
On peut également déduire la coudée de la pyramide elle-même. Tous les égyptologues s’accordent à dire qu’elle mesure 440 CR de côté et 280 CR de hauteur, il suffit de mesurer un côté en mètre et de le diviser par 440 pour obtenir une estimation de la coudée royale utilisée pour cette construction. Il y a eu plusieurs campagnes de mesure menées par Flinders Petrie, JF Cole, Lehner et Goodman, Glen Dash ou encore Gilles Dormion, qui a déjà mesurer la chambre haute. La mesure la plus basse obtenue est 230,25 mètres et la plus haute est 230,45 mètres. Ce qui nous donne une coudée royale de 0,5232m (230,25 ÷ 440 = 0,52329) pour la valeur la plus basse et 0,5237m (230,45 ÷ 45 = 0,52375) pour la valeur la plus haute.
En plus de ces mesures, il y a une théorie qui a été émise en 1952 par Charles Funck-Hellet dans la revue du Caire qui dit que la coudée royale a été choisie pour des raisons mathématiques, car il se trouve que Pi divisé par 6 donne une valeur de la coudée tout à fait acceptable (𝛑 ÷ 6 = 0,523598775598299).
Pour le moment on a 3 estimations de la coudée royale, une déduite de la chambre haute (0,5235m), une déduite de la dimension de la pyramide (0,5232m) et une issue de la théorie mathématiques (0,523598775598299m). Avant de commencer les calculs, j’aimerai ajouter une quatrième valeur, car le reproche le plus récurrent fait aux chercheurs indépendants, c’est qu’ils choisissent les mesures qui les arrangent pour ensuite y trouver des résultats incroyable. Personnellement je n’ai pas vraiment de point de vue à défendre, alors je vais faire les calculs avec plusieurs valeur de coudées royales, j’esquive déjà un reproche 😉
Sur le blog d’une personne plutôt véhémente dont je ne veux pas faire la promotion, j’ai lu ceci à propos du choix de la coudée : « En se basant sur une coudée royale estimée dans les années 50 par l’égyptologue Jean-Philippe Lauer entre 52.35 et 52.4 cm, ce docteur a choisit arbitrairement d’estimer la coudée royale égyptienne à 52.36 cm, ce qui va du coup forcément l’arranger pour en déduire un certain nombre de corrélations qu’il va pouvoir trouver entre le nombre PI, le nombre d’or, la coudée royale et le mètre car c’est bien ici cela le but de la manœuvre. Si le but était par exemple de faire une simple moyenne, il était plus juste de choisir 52.375 cm. »
Et bien je vais prendre la proposition de cette personne en utilisant une coudée royale moyenne de 0,52375m.
Pi et le nombre d’or dans la pyramide
Si vous voulez vous amuser avec les calculs et les valeurs de coudée royale, vous pouvez télécharger le tableur sous 3 formats :
Nous avons donc 4 valeurs de coudée royale.
- Valeur 1 : déduction de la chambre haute (dite du roi) d’après les mesures de l’architecte Gilles Dormion.
- Valeur 2 : résultat de 𝛑 ÷ 6 d’après la théorie avancée par Charles Funck-Hellet.
- Valeur 3 : déduction de la dimension du côté de la pyramide. La valeur choisie est la valeur extrême basse (230,25m).
- Valeur 4 : trouvée sur un blog, c’est la moyenne de la fourchette proposée par l’égyptologue Jean-Philippe Lauer. Il estimait que le coudée royale faisait entre 52.35 cm et 52.4 cm.
Avec ces 4 valeurs, nous pouvons calculer les dimensions de la pyramide de Kheops en mètre.
| ____ | Coudée Royale (mètre) | Base (mètre) | Hauteur (mètre) | Apothème (mètre) | Diagonale de la base (mètre) | Arrête (mètre) |
| v1 | 0,5235 | 230,34 | 146,58 | 186,413050240588 | 325,749951957019 | 219,120866646698 |
| v2 | 0,523598775598299 | 230,383461263252 | 146,607657167524 | 186,448223231168 | 325,811415464948 | 219,162211049187 |
| v3 | 0,5232 | 230,208 | 146,496 | 186,306223277699 | 325,563275766785 | 218,995295949479 |
| v4 | 0,52375 | 230,45 | 146,65 | 186,502072709662 | 325,90551544888 | 219,22550889438 |
Ensuite voilà les valeurs attendues. Ces tableaux servent principalement à calculer la marge d’erreur entre le résultat d’un calcul et la valeur attendue.
| Pi | 3,14159265358979 |
| Phi | 1,61803398874989 |
| Constante de Ramanujan-Soldner | 1,45136923488338 |
| Constante de Brun (B₂) | 1,902160582538 |
| Constante d’Aladi-Grinstead | 0,8093940205 |
| Constante de Neper (e) | 2,71828182845904 |
| Constante de Neper 100*(e) | 271,828182845904 |
Allez maintenant on passe aux choses sérieuses, voilà les calculs qui permettent de trouver des constantes mathématiques au sein de la pyramide de Kheops.
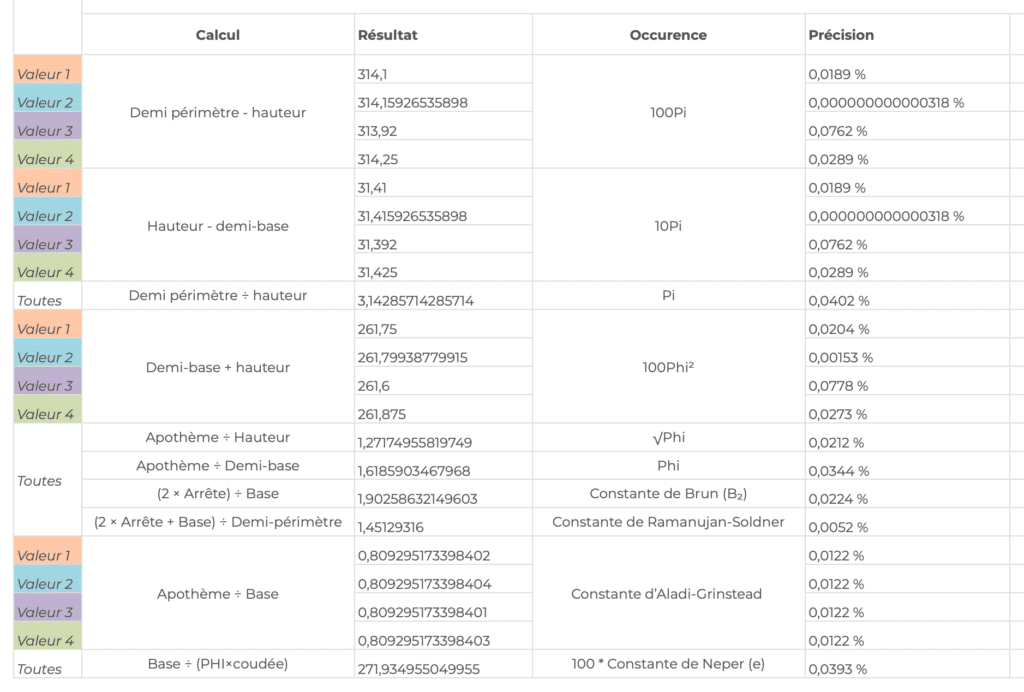
Si vous avez besoin de plus de lisibilité, vous pouvez télécharger les fichiers sources ici :
Hasard ou volonté ?
Normalement la première question qu’on se pose c’est : « est-ce que c’est du pur hasard ou les égyptiens on vraiment voulu inclure tous ces nombres ? » Plutôt que de répondre en écrivant un pavé sans fin, je vous invite à regarder la vidéo sur le sujet, j’y aborde des problématiques dont je n’ai pas parlé dans cet article et j’essaie de répondre à cette fameuse question du hasard. Bon visionnage 🍿





Bonjour,
Phi et Pi sont des rapports. Quelque soit l’unité choisie, si on trouve Pi ou Phi, alors c’est qu’on a un rapport. Le mètre ni la coudée n’ont aucun lien avec le résultat et il faudrait re-rédiger l’article pour expliciter cela : Quelle que soit la pyramide, ces rapports existent, car ils sont inhérents à des figures géométriques…
Si on cherche une inconnue, « x », il faut créer un rapport.
Par exemple, si on cherche la longueur de la coudée royale, il faut postuler qu’elle est d’efférente de 1 mètre… Si on trouve des trucs magiques en mètre, soit c’est du bidon, soit c’est un rapport qui resterait vrai avec une coudée de disons 1,23 point didot.
Postulons que la mesure de la coudée a été utilisée pour créer une vide royale dans la chambre du roi de la pyramide, et que les mesures avaient « besoin » d’être « justes » (en coudées).
Alors il ne faut pas choisir de faire des mesures en mètres, mais en « x »… Il suffit de trouver toutes les valeurs x qui satisfont Largeur et Longueur et hauteur sont entier ou multiples… Et comme c’est « sacré » qu’ils respectent une certaine harmonie (PI, Phi ou tout autre rapport « magique »).
Cdlt,
François-Joseph Deminière.
Bonjour,
absolument géniale cette vidéo : sur le fond, très bien argumenté, et aussi la forme (très à l’aise, et un mix sérieux-humour bien dosé)
Merci beaucoup pour ça.
Pyramidement,
Stéphane Gautard.
Très bonne vidéo